Sixteen weeks

Source: 3News, November 17 2020

 

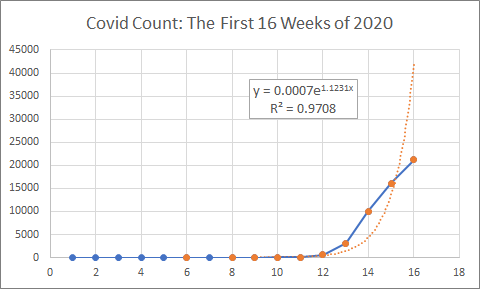
Exponential growth?

In the neighborhood of exponential, yeah.

Excel wouldn't let me add the exponential trendline until I eliminated the zero values.

The trendline is based on the orange (non-zero) dots.

//

Covid Deaths by week for 2020. I want to leave out the word "deaths" so as not to emphasize the unpleasantness of the topic. Every other week shown:

Week 6:	1
Week 8:	5
Week 10:	35
Week 12:	571
Week 14:	10,012
Week 16:	17,067

What makes a series of numbers "exponential" is that it doubles at regular intervals, every week or every year, for example.

Suppose the Covid number doubles every week, and starts at Week 6 with one death. Then we expect two in week 7 and four in week 8. Four is close to the reported count of 5, so our guess, and the reported number, seem reasonable. 

No deaths were reported in Week 7. Does that seem odd? I don't think so. An exponential sequence of numbers is only an estimate or prediction, at least as I use it here. Anyway, zero is pretty close to 2.

Starting with one in Week 6 and doubling weekly, we see four in Week 8, eight in week 9, and 16 in Week 10. Deaths reported for Week 10 were 35, more than twice our estimate of 16. Let's go with the reported number.

Our estimate: 35 in Week 10, 70 in Week 11, 140 in Week 12. The reported number for Week 12 is 571. Our estimate is way low. It is likely that our "weekly doubling" assumption is incorrect. It is also possible that the arithmetic requires unrealistic counts (unrealistic, like 1.8 deaths, say).

It is also possible that the reported numbers are incorrect. Certainly the reports could be based on the best information available (and I assume they are) and entered and checked carefully (and I assume they are) and still differ from "God's count". And sometimes people do mess with the numbers for their own reasons, or tally the numbers their own way for whatever reason. But dead is dead, and that's not an easy thing to hide. I trust the reported numbers, same as I do with economic data.

Let's revise our estimate. Let's say the 35 deaths reported in Week 10 is correct. The Week 12 number is 571. How many doublings does it take to get from 35 to 571?

35 ... 70 ... 140 ... 280 ... 560 

560 is close to 571. It takes four doublings to get there. Four doublings in two weeks. So in these weeks it appears that the "doubling time" of the exponential process is about 3½ days rather than a week.

How about going from Week 12 to Week 14? From 571 to 10,012?

571 ... 1142 ... 2284 ... 4568 ... 9136 

Four doublings gets us in the neighborhood of 10,012. Five would get us to 18,272 and that's way above the reported number. Four doublings, then, for weeks 12 to 14, the same as for weeks 10 to 12. So my confidence in that doubling time improves.

For the first few weeks we used a 7-day doubling time. Then for the next few weeks the doubling time looks more like 3.5 days. What happened?

Could be that Covid deaths were under-reported in the early weeks, when people were still learning what they were dealing with. That seems realistic to me. That, and the early numbers were so very small that if they're off just a little, the error is still a big percentage. But then, when you get to the bigger numbers and higher death counts, the same (big percentage) error is much easier to see.

Or it could be that the easily-transmitted virus mutated and became even more easily transmitted. This could account for it, and again it could have been missed in the early days, but this explanation seems less "occam" simple. Besides, there was no talk of mutation in the early days of the pandemic. Also, it seems that this possibility could be checked by comparing concurrent data from other nations. Seems to me if mutation in the early weeks reduced the doubling time, we'd have heard about it by now.

Could be that I made a sloppy guess and didn't check it enough. I think that's what happened.

I should say, I'm no expert. I just find it interesting to look at numbers and think about how they came to be. And evidently, I have more thoughts on this topic than I realized.

If I miss anything that seems to you worth mentioning, don't hesitate to mention it.

From Week 14 to Week 16, the reported numbers don't even double once. We jump from 10 thousand to 17 thousand deaths in that two week period. Based on the reported numbers, the "rule of 70" gives me a doubling time of 16.7 days. When I try to figure it I get 17.9 days. Either way, about 2½ weeks. That's the slowest doubling time so far, slower even than in the first few weeks. What happened?

I think the slower doubling time -- the slower spread of Covid -- came about because we learned how to deal with the problem: the hand-washing, the social distancing, and, you know, shutting down the economy and wearing masks.

//

The first US death from Covid was on Thursday, February 6, the sixth Thursday of the year. Week six.

On Wednesday, March 11, the NBA suspended game play until further notice. Week 11.

According to AJMC, on March 13, the Trump administration declared Covid 19 a national emergency and issued a travel ban. Assuming that the first Saturday of the year is the end of the first week of the year, Friday, March 13 was in Week 11.

On March 19, California became the first state to issue a stay-at-home order. Week 12. [AJMC]

On March 25, "Mathematical models based on social distancing measures implemented in Wuhan, China, show keeping tighter measures in place for longer periods of time can flatten the COVID-19 curve." Week 13. [AJMC]

On April 16, "After Trump briefly entertains the idea of reopening the US economy in time for Easter Sunday, the White House releases broad guidelines for how people could return to work, to church, and to restaurants and other venues. The plan outlines the concept of “gating criteria,” which call for states or metropolitan areas to achieve benchmarks in reducing COVID-19 cases or deaths before taking the next step toward reopening." Week 16. [AJMC]

Wikipedia lists 23 states that lifted stay-at-home orders or advisories between April 26 (Week 18) and June 11 (Week 24).